3197. Find the Minimum Area to Cover All Ones II #2086
-
|
Topics: You are given a 2D binary array Return the minimum possible sum of the area of these rectangles. Note that the rectangles are allowed to touch. Example 1:
Example 2:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to find the minimum total area of three non-overlapping rectangles that cover all the 1's in a given binary grid. The rectangles must have horizontal and vertical sides and can touch but not overlap. The solution involves enumerating all possible ways to split the grid into three regions using horizontal and vertical lines, then calculating the sum of the areas of the bounding boxes of the 1's in each region. Approach
Let's implement this solution in PHP: 3197. Find the Minimum Area to Cover All Ones II <?php
/**
* @param Integer[][] $grid
* @return Integer
*/
function minimumSum($grid) {
$m = count($grid);
$n = count($grid[0]);
$ones = [];
for ($i = 0; $i < $m; $i++) {
for ($j = 0; $j < $n; $j++) {
if ($grid[$i][$j] == 1) {
$ones[] = [$i, $j];
}
}
}
$calculateArea = function($points) {
if (empty($points)) return 0;
$minRow = PHP_INT_MAX;
$maxRow = PHP_INT_MIN;
$minCol = PHP_INT_MAX;
$maxCol = PHP_INT_MIN;
foreach ($points as $p) {
$minRow = min($minRow, $p[0]);
$maxRow = max($maxRow, $p[0]);
$minCol = min($minCol, $p[1]);
$maxCol = max($maxCol, $p[1]);
}
return ($maxRow - $minRow + 1) * ($maxCol - $minCol + 1);
};
$ans = PHP_INT_MAX;
for ($i = 0; $i < $m - 1; $i++) {
for ($j = $i; $j < $m - 1; $j++) {
$s1 = array_filter($ones, function($p) use ($i) { return $p[0] <= $i; });
$s2 = array_filter($ones, function($p) use ($i, $j) { return $p[0] > $i && $p[0] <= $j; });
$s3 = array_filter($ones, function($p) use ($j) { return $p[0] > $j; });
if (count($s1) == 0 || count($s2) == 0 || count($s3) == 0) continue;
$area = $calculateArea($s1) + $calculateArea($s2) + $calculateArea($s3);
if ($area < $ans) $ans = $area;
}
}
for ($i = 0; $i < $n - 1; $i++) {
for ($j = $i; $j < $n - 1; $j++) {
$s1 = array_filter($ones, function($p) use ($i) { return $p[1] <= $i; });
$s2 = array_filter($ones, function($p) use ($i, $j) { return $p[1] > $i && $p[1] <= $j; });
$s3 = array_filter($ones, function($p) use ($j) { return $p[1] > $j; });
if (count($s1) == 0 || count($s2) == 0 || count($s3) == 0) continue;
$area = $calculateArea($s1) + $calculateArea($s2) + $calculateArea($s3);
if ($area < $ans) $ans = $area;
}
}
for ($k = 0; $k < $n - 1; $k++) {
$left = array_filter($ones, function($p) use ($k) { return $p[1] <= $k; });
$right = array_filter($ones, function($p) use ($k) { return $p[1] > $k; });
if (count($left) == 0 || count($right) == 0) continue;
for ($i = 0; $i < $m - 1; $i++) {
$s1 = array_filter($left, function($p) use ($i) { return $p[0] <= $i; });
$s2 = array_filter($left, function($p) use ($i) { return $p[0] > $i; });
if (count($s1) == 0 || count($s2) == 0) continue;
$area = $calculateArea($s1) + $calculateArea($s2) + $calculateArea($right);
if ($area < $ans) $ans = $area;
}
}
for ($k = 0; $k < $n - 1; $k++) {
$left = array_filter($ones, function($p) use ($k) { return $p[1] <= $k; });
$right = array_filter($ones, function($p) use ($k) { return $p[1] > $k; });
if (count($left) == 0 || count($right) == 0) continue;
for ($i = 0; $i < $m - 1; $i++) {
$s1 = array_filter($right, function($p) use ($i) { return $p[0] <= $i; });
$s2 = array_filter($right, function($p) use ($i) { return $p[0] > $i; });
if (count($s1) == 0 || count($s2) == 0) continue;
$area = $calculateArea($left) + $calculateArea($s1) + $calculateArea($s2);
if ($area < $ans) $ans = $area;
}
}
for ($i = 0; $i < $m - 1; $i++) {
$top = array_filter($ones, function($p) use ($i) { return $p[0] <= $i; });
$bottom = array_filter($ones, function($p) use ($i) { return $p[0] > $i; });
if (count($top) == 0 || count($bottom) == 0) continue;
for ($k = 0; $k < $n - 1; $k++) {
$s1 = array_filter($top, function($p) use ($k) { return $p[1] <= $k; });
$s2 = array_filter($top, function($p) use ($k) { return $p[1] > $k; });
if (count($s1) == 0 || count($s2) == 0) continue;
$area = $calculateArea($s1) + $calculateArea($s2) + $calculateArea($bottom);
if ($area < $ans) $ans = $area;
}
}
for ($i = 0; $i < $m - 1; $i++) {
$top = array_filter($ones, function($p) use ($i) { return $p[0] <= $i; });
$bottom = array_filter($ones, function($p) use ($i) { return $p[0] > $i; });
if (count($top) == 0 || count($bottom) == 0) continue;
for ($k = 0; $k < $n - 1; $k++) {
$s1 = array_filter($bottom, function($p) use ($k) { return $p[1] <= $k; });
$s2 = array_filter($bottom, function($p) use ($k) { return $p[1] > $k; });
if (count($s1) == 0 || count($s2) == 0) continue;
$area = $calculateArea($top) + $calculateArea($s1) + $calculateArea($s2);
if ($area < $ans) $ans = $area;
}
}
return $ans;
}
// Test cases
$grid1 = [[1,0,1],[1,1,1]];
echo minimumSum($grid1) . PHP_EOL; // 5
$grid2 = [[1,0,1,0],[0,1,0,1]];
echo minimumSum($grid2) . PHP_EOL; // 5
?>Explanation:
This approach efficiently explores all possible configurations of three non-overlapping rectangles by leveraging the constraints of the grid size, ensuring optimal performance while guaranteeing the correct solution. |
Beta Was this translation helpful? Give feedback.
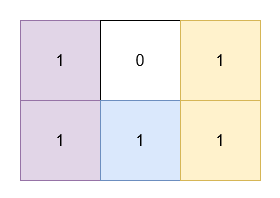
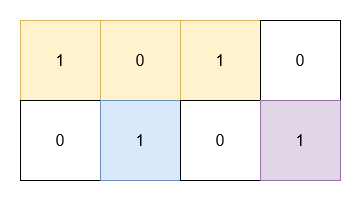
We need to find the minimum total area of three non-overlapping rectangles that cover all the 1's in a given binary grid. The rectangles must have horizontal and vertical sides and can touch but not overlap. The solution involves enumerating all possible ways to split the grid into three regions using horizontal and vertical lines, then calculating the sum of the areas of the bounding boxes of the 1's in each region.
Approach
(max_row - min_row + 1) * (max_col - min_c…