3459. Length of Longest V-Shaped Diagonal Segment #2102
-
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to find the longest V-shaped diagonal segment in a 2D grid where the segment starts with 1, followed by the sequence 2, 0, 2, 0, etc., and can make at most one clockwise 90-degree turn. The solution involves using dynamic programming to precompute the lengths of valid segments in all four diagonal directions both with and without turns. Approach
Let's implement this solution in PHP: 3459. Length of Longest V-Shaped Diagonal Segment <?php
/**
* @param Integer[][] $grid
* @return Integer
*/
function lenOfVDiagonal($grid) {
$n = count($grid);
$m = count($grid[0]);
$dirs = [
[1, 1], // d0: top-left to bottom-right
[1, -1], // d1: top-right to bottom-left
[-1, -1], // d2: bottom-right to top-left
[-1, 1] // d3: bottom-left to top-right
];
$dp = array_fill(0, 4, array_fill(0, $n, array_fill(0, $m, 0)));
$rev_dp = array_fill(0, 4, array_fill(0, $n, array_fill(0, $m, 0)));
// Compute dp for direction 0
for ($r = 0; $r < $n; $r++) {
for ($c = 0; $c < $m; $c++) {
if ($grid[$r][$c] == 1) {
$dp[0][$r][$c] = 1;
} else {
$pr = $r - $dirs[0][0];
$pc = $c - $dirs[0][1];
if ($pr >= 0 && $pr < $n && $pc >= 0 && $pc < $m && $dp[0][$pr][$pc] > 0) {
$expected = ($dp[0][$pr][$pc] % 2 == 1) ? 2 : 0;
if ($grid[$r][$c] == $expected) {
$dp[0][$r][$c] = $dp[0][$pr][$pc] + 1;
}
}
}
}
}
// Compute dp for direction 1
for ($r = 0; $r < $n; $r++) {
for ($c = $m - 1; $c >= 0; $c--) {
if ($grid[$r][$c] == 1) {
$dp[1][$r][$c] = 1;
} else {
$pr = $r - $dirs[1][0];
$pc = $c - $dirs[1][1];
if ($pr >= 0 && $pr < $n && $pc >= 0 && $pc < $m && $dp[1][$pr][$pc] > 0) {
$expected = ($dp[1][$pr][$pc] % 2 == 1) ? 2 : 0;
if ($grid[$r][$c] == $expected) {
$dp[1][$r][$c] = $dp[1][$pr][$pc] + 1;
}
}
}
}
}
// Compute dp for direction 2
for ($r = $n - 1; $r >= 0; $r--) {
for ($c = $m - 1; $c >= 0; $c--) {
if ($grid[$r][$c] == 1) {
$dp[2][$r][$c] = 1;
} else {
$pr = $r - $dirs[2][0];
$pc = $c - $dirs[2][1];
if ($pr >= 0 && $pr < $n && $pc >= 0 && $pc < $m && $dp[2][$pr][$pc] > 0) {
$expected = ($dp[2][$pr][$pc] % 2 == 1) ? 2 : 0;
if ($grid[$r][$c] == $expected) {
$dp[2][$r][$c] = $dp[2][$pr][$pc] + 1;
}
}
}
}
}
// Compute dp for direction 3
for ($r = $n - 1; $r >= 0; $r--) {
for ($c = 0; $c < $m; $c++) {
if ($grid[$r][$c] == 1) {
$dp[3][$r][$c] = 1;
} else {
$pr = $r - $dirs[3][0];
$pc = $c - $dirs[3][1];
if ($pr >= 0 && $pr < $n && $pc >= 0 && $pc < $m && $dp[3][$pr][$pc] > 0) {
$expected = ($dp[3][$pr][$pc] % 2 == 1) ? 2 : 0;
if ($grid[$r][$c] == $expected) {
$dp[3][$r][$c] = $dp[3][$pr][$pc] + 1;
}
}
}
}
}
// Compute rev_dp for direction 0
for ($r = $n - 1; $r >= 0; $r--) {
for ($c = $m - 1; $c >= 0; $c--) {
$rev_dp[0][$r][$c] = 1;
$nr = $r + $dirs[0][0];
$nc = $c + $dirs[0][1];
if ($nr >= 0 && $nr < $n && $nc >= 0 && $nc < $m) {
$nextVal = nextValue($grid[$r][$c]);
if ($grid[$nr][$nc] == $nextVal) {
$rev_dp[0][$r][$c] += $rev_dp[0][$nr][$nc];
}
}
}
}
// Compute rev_dp for direction 1
for ($r = $n - 1; $r >= 0; $r--) {
for ($c = 0; $c < $m; $c++) {
$rev_dp[1][$r][$c] = 1;
$nr = $r + $dirs[1][0];
$nc = $c + $dirs[1][1];
if ($nr >= 0 && $nr < $n && $nc >= 0 && $nc < $m) {
$nextVal = nextValue($grid[$r][$c]);
if ($grid[$nr][$nc] == $nextVal) {
$rev_dp[1][$r][$c] += $rev_dp[1][$nr][$nc];
}
}
}
}
// Compute rev_dp for direction 2
for ($r = 0; $r < $n; $r++) {
for ($c = 0; $c < $m; $c++) {
$rev_dp[2][$r][$c] = 1;
$nr = $r + $dirs[2][0];
$nc = $c + $dirs[2][1];
if ($nr >= 0 && $nr < $n && $nc >= 0 && $nc < $m) {
$nextVal = nextValue($grid[$r][$c]);
if ($grid[$nr][$nc] == $nextVal) {
$rev_dp[2][$r][$c] += $rev_dp[2][$nr][$nc];
}
}
}
}
// Compute rev_dp for direction 3
for ($r = 0; $r < $n; $r++) {
for ($c = $m - 1; $c >= 0; $c--) {
$rev_dp[3][$r][$c] = 1;
$nr = $r + $dirs[3][0];
$nc = $c + $dirs[3][1];
if ($nr >= 0 && $nr < $n && $nc >= 0 && $nc < $m) {
$nextVal = nextValue($grid[$r][$c]);
if ($grid[$nr][$nc] == $nextVal) {
$rev_dp[3][$r][$c] += $rev_dp[3][$nr][$nc];
}
}
}
}
$ans = 0;
for ($r = 0; $r < $n; $r++) {
for ($c = 0; $c < $m; $c++) {
for ($d = 0; $d < 4; $d++) {
$L = $dp[$d][$r][$c];
if ($L > 0) {
if ($L > $ans) {
$ans = $L;
}
$d2 = ($d + 1) % 4;
$nr = $r + $dirs[$d2][0];
$nc = $c + $dirs[$d2][1];
if ($nr >= 0 && $nr < $n && $nc >= 0 && $nc < $m) {
$expected = ($L % 2 == 1) ? 2 : 0;
if ($grid[$nr][$nc] == $expected) {
$total = $L + $rev_dp[$d2][$nr][$nc];
if ($total > $ans) {
$ans = $total;
}
}
}
}
}
}
}
return $ans;
}
/**
* @param $v
* @return int
*/
function nextValue($v) {
if ($v == 1) return 2;
if ($v == 2) return 0;
if ($v == 0) return 2;
return -1;
}
// Test cases
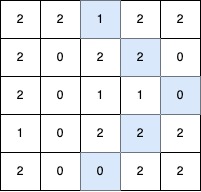
$grid1 = [[2,2,1,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]];
echo lenOfVDiagonal($grid1); // Output: 5
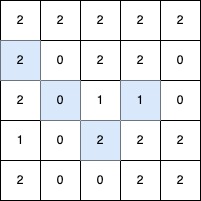
$grid2 = [[2,2,2,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]];
echo lenOfVDiagonal($grid2); // Output: 4
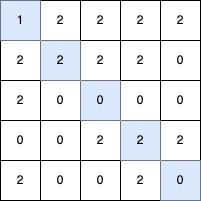
$grid3 = [[1,2,2,2,2],[2,2,2,2,0],[2,0,0,0,0],[0,0,2,2,2],[2,0,0,2,0]];
echo lenOfVDiagonal($grid3); // Output: 5
$grid4 = [[1]];
echo lenOfVDiagonal($grid4); // Output: 1
?>Explanation:
This approach efficiently computes the longest V-shaped diagonal segment by leveraging dynamic programming to explore all possible segments and turns, ensuring optimal performance even for large grids. |
Beta Was this translation helpful? Give feedback.
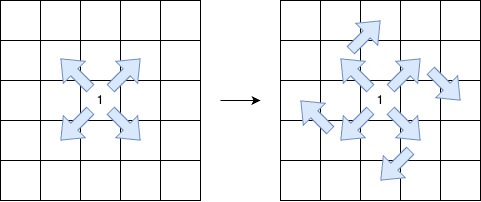
We need to find the longest V-shaped diagonal segment in a 2D grid where the segment starts with 1, followed by the sequence 2, 0, 2, 0, etc., and can make at most one clockwise 90-degree turn. The solution involves using dynamic programming to precompute the lengths of valid segments in all four diagonal directions both with and without turns.
Approach
dpandrev_dp, of dimensions 4 x n x m. Thedparray stores the lengths of segments starting from each cell in each direction without any turns. Therev_dparray stores the lengths of segm…